Solutions manual for NTB - 1.1 Divisibility and primality
Exercise 1.1. Let
with
. Show that
if and only if
. Proof
(q.e.d).
Exercise 1.2. Let
be a composite integer. Show that there exists a prime
dividing
with
. Proof We use strong induction. Let
be the proposition that for all composite integer
, there exists a prime
dividing
with
. Base case:

is true. Inductive step: Now we must show that
imply
for all composite integer
. Since
is a composite, there exists
so that
with
(if
, we just swap them). If
is a prime, then
is true since
divides
and
. If
is a composite, then according to the induction assumption, there exists a prime
that divides
. This prime
also divides
with
. So P(n) is true. Therefore, the claim is true by strong induction for all composite integer n (q.e.d).
Exercise 1.3. Let
be a positive integer. Show that for every real number
, the number of multiples of
in the interval
is
; in particular, for every integer
, the number of multiples of
among
is
. Proof * The first claim: applying Theorem 1.4 with
and
, we have: there exits unique
such that
. It's easy to see that
is the number of multiples of m in the interval
. Page 4 of NTB shows that
. By the first claim of Exercise 1.5, we know that
, which proves the claim. * The second claim: just apply the first claim with
, we have
with
(q.e.d).
Exercise 1.4. Let
. Show that
. Proof Let
with
. In other words, there exists
so that
. We have:
, which proves the first inequality. For the second inequality, observes that
and
for all
and
. We have:
, which proves the inequality (q.e.d).
Exercise 1.5. Let
and
with
. Show that
; in particular
for all positive integers
. Proof We prove a stronger claim (which is copied from [Graham, Knuth, Patashnik]). Consider function

with

and

. It's easy to see that f is a continuous, monotonically increasing function with the property:

= integer then

is a integer. We claim that
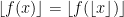
. Let's prove it. If

, then there's nothing to prove. Otherwise

, then we have

, since f is increasing. Hence

, since

is nondecreasing. If

, then there must be a number y such that

and

, since f is continuous. This y is an integer, because of

's special property. But there can not an integer strictly betweet

and

. This contradiction implies that we must have

, which proves the claim. Applying this claim to Exercise 1.5, we got what we want to prove (q.e.d).
Exercise 1.6. Let
with
. Show that
.
Exercise 1.7. Show that Theorem 1.5 also holds for the interval
. Does it hold in general for the intervals
or
?
