Solutions manual for NTB - 1.2 Ideals and greatest common divisors

Exercise 1.8. Let

be a non-empty set of integers that is closed under addition (i.e.,

for all

). Show that

is an ideal if and only if

for all

. Proof We prove

is an ideal implies

for all

and vice versa. First, we show

is an ideal implies

for all

. Since

is an ideal so we have

for all

. Choose

, we get what we want to prove. Now, we show

for all

implies

is an ideal. For all

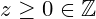
, we have

(

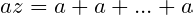
times

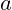
) which belongs to

since

is closed under addition. Similarly, for all

, we have

(

times

) which belongs to

since

is closed under addtion and

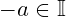
. So we have

for all

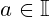
and for all

. This proves

is an ideal.(q.e.d.)

---

Exercise 1.9. Show that for all integers

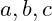
, we have: (a)

; (b)

; (c)

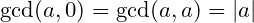
and

; (d)

. Proof a, b, c are trivial and can be easily derived from the definition of greatest command divisor. We prove only d here. We first show that

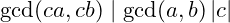
. According to Theorem 1.8, there exist

such that

. Then we have

. Then once again, according to thereom 1.8, we have

. Now we show that

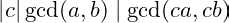
. Since

and

, we have

and

. Hence

is a common divisor of

and

. That means

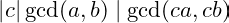
.Thus

.(q.e.d.)

---

Exercise 1.10. Show that for all integers

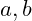
with

, we have

. Proof We use proof by contradiction. Suppose

. Then we have

and

. Hence

and

. That means

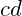
is a common divisor of

and

. But

. This is a contradiction. Therefore,

. (q.e.d.)

---

Exercise 1.11. Let

be an integer. Show that if

are relatively prime integers, each of which divides

, then

divides

. Proof Before proving it, let's pause for a second and think about this problem. Is it just me or this problem is right by intuition? After two months studying number theory, I can tell you that not only this problem but most problems in this field are intuitively right. May this be the reason why number theory is so beautiful. Everybody can intuitively get it, but only somebody can intellectually prove it. So how do we solve this exercise? Well, we have

so let

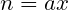
for some

. We claim that

, hence

. To prove

, observes that

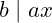
and

, then applying Theorem 1.9, we got what we want to prove. (q.e.d.)

---

Exercise 1.12. Show that two integers are relatively prime if and only if there is no one prime that divides both of them. Proof (This proof left blank because it is way too trivial) (q.e.d.)

---

Exercise 1.13. Let

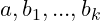
be integers. Show that

if and only if

for

. Proof We show

implies

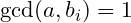
for

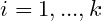
and vice versa. First we show

implies

for

. We prove this by contradiction. Suppose

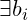
such that

. We have

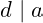
and

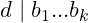
. Hence

is a common divisor of

and

. That means

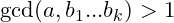
. This is a contradiction. Therefore,

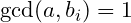
for

. Now we show

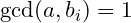
for

implies

. Applying exercise 2.12, we see that there's no prime divides both

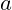
and

for

. That means there's no prime divides both

and

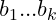
. Hence they are relatively prime. (q.e.d.)

---

Exercise 1.14. Let

be a prime and

an integer, with

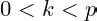
. Show that the binomial cofficient

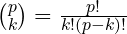
, which is an integer, is divisible by

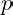
. Proof We have:

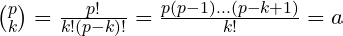
for some

. Since

, then we have

. Hence

. That means

for some

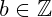
. Therefore,

.(q.e.d.)

---

Exercise 1.15. An integer

is called square-free if it is not divisible by the square of any integer greater than 1. Show that: (a)

is square-free if and only if

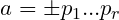
, where the

’s are distinct primes; (b) every positive integer

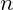
can be expressed uniquely as

, where

and

are positive integers, and

is square-free. Proof (q.e.d.)