Solutions manual for NTB - 1.3 Some consequences of unique factorization
Let's recall some notations and facts before we begin. For each prime

, we may define the function

, mapping non-zero integers to non-negative integers, as follows: for every integer

, if
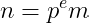
, where

, then
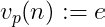
. We may then write the factorization of

into primes as:

, where the product is over all primes p; although syntactically this is an infinite product, all but finitely many of its terms are equal to 1, and so this expression makes sense. Observe that if

and

are non-zero integers, then

for all primes
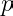
, and
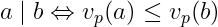
for all primes

. From this, it is clear that:


. The greatest common divisor of

is denoted

and is the unique non-negative integer

satisfying

for all primes

. The least common multiple of

is denoted

and is the unique non-negative integer

satisfying

for all primes
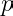
.
Exercise 1.19. Let n be an integer. Generalizing Exercise 1.11, show that if

is a pairwise relatively prime family of integers, where each

divides

, then their product

also divides
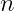
.Proof We have:
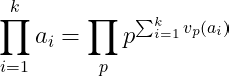
Since

is a pairwise relatively prime family of integers, for all primes
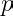
, we have:
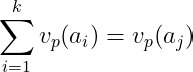
, for some
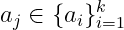
. (1)Since

, hence

for all primes

. (2) From (1) and (2), we see that

must divides

. (q.e.d)
Exercise 1.20. Show that for all integers

,
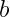
,

, we have: (a)

, (b)

, (c)

, (d)

. Proof a, b, c are trivial and can be easily derived from the definition of least command multiple. We prove only d here:
(q.e.d)
Exercise 1.21. Show that for all integers

,
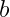
, we have: (a)
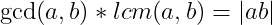
; (b)

. Proof (a) Observe that:
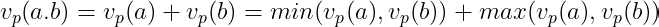
for all primes
. (b) This directly follows from (a). (q.e.d)
Exercise 1.22. Let

with
. Show that: (a)
; (b)
. Proof (Intentionally left blank) (q.e.d)
Exercise 1.23. Let

with

. Show that

; in particular, there exist integers

such that
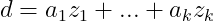
. Proof We can prove this by generalizing Theorem 1.7 to many integers. Observe that each

is an ideal of
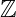
, and so is their sum

. Let

is an ideal of

such that

. According to Theorem 1.6, there exists an unique integer

such that
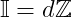
. We show that
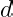
is indeed the greatest common divisor of

. Note that

. Since
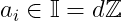
, we see that

for

. So we see that

is a common divisor of

. Since

, there exist integers
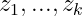
such that
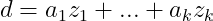
. Now suppose

is another common divisor of

with

. Then the equation
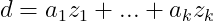
implies that

, which says that
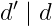
. Thus, any common divisor

of

divides
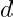
. That proves that

is a greatest common divisor of

. (q.e.d)
Exercise 1.24. Show that if

is a pairwise relatively prime family of integers, then
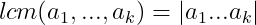
. Proof Since

is a pairwise relative prime family of integers, we see that for all primes

,

for some

, and
for all

. Hence we see that for all primes

,

for some

. Therefore,
(q.e.d)
Exercise 1.25. Show that every non-zero

can be expressed as:

, where the
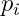
’s are distinct primes and the

’s are non-zero integers, and that this expression in unique up to a reordering of the primes. Proof We know that we can represent every non-zero

as a fraction of the form

where

and

are relatively prime; moreover, the values of
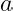
and
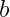
are uniquely determined up to sign. Applying Theorem 1.3 (the fundamental theorem of arithmetic) and the fact that

and

are relatively prime, we see that:

where
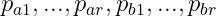
are distinct primes and

are positive integers. Moreover, this expression is unique, up to a reordering of the primes. (q.e.d)
Exercise 1.26. Let

and

be positive integers, and suppose

such that

for some

. Show that

. In other words,

is either an integer or is irrational. Proof Using Exercise 1.25's result, we have:

, where the

’s are distinct primes and the
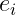
’s are non-zero integers, and that this expression in unique up to a reordering of the primes. To prove

, we must show that
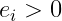
for all

. Since

for some positive integers

and

, we see that:

. According to Theorem 1.3, we see that

are positive integers. Since
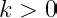
, that means

for all

, which proves our claim. (q.e.d)
