Solutions manual for NTB - 3.3. Basic integer arithmetic
Let's review some notations and facts. For an integer

, we define its bit length, or simply, its length, which we denote by
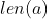
, to be the number of bits in the binary representation of
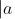
; more precisely,
If
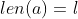
, we say that

is an
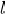
-bit integer. Notice that if

is a positive,
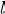
-bit integer, then
, or equivalently,
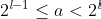
.
Let a and b be arbitrary integers. Then we have:
(i) We can compute
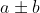
in time
.
(ii) We can compute
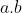
in time
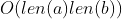
.
Let a and b be arbitrary integers. Then we have:
(i) We can compute
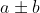
in time
.
(ii) We can compute
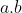
in time
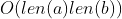
.
(iii) If
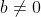
, we can compute the quotient
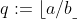
and the remainder
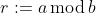
in time
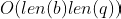
.
Exercise 3.24. Let
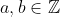
with
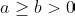
, and let
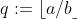
. Show that:
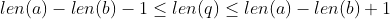
Proof
If you look at the list of errata, you'll see that I found a stronger version of this exercise. My proof is as following.
We see that
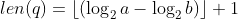
. Hence what we need to prove is:
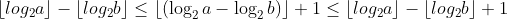
which is the same as proving:
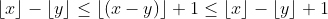
for some
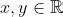
which in turn can be proved by using this fact:
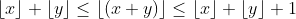
for all
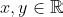
.
(q.e.d.)
Exercise 3.25. Let
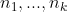
be postivie integers. Show that:
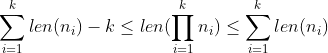
Proof
As in Exercise 3.24, I think I found a slightly better version of this exercise as follows:
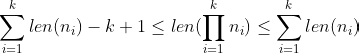
We can prove it using the same technique as the proof of Exercise 3.24. We see that:
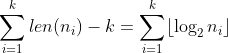
,
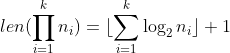
,
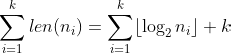
Since we have
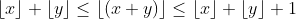
for all
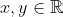
, we see that:
and,
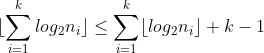
.
(q.e.d.)
Exercise 3.26. Show that given integers
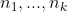
, with each
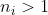
, we can compute the product
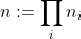
in time
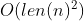
.
Proof
(q.e.d.)
Exercise 3.27. Show that given integers
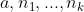
, with each
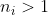
, where
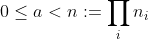
, we can compute
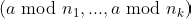
in time
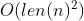
.
Proof
(q.e.d.)
Exercise 3.28. Show that given integers
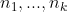
, with each
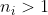
, we can compute
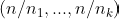
, where
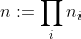
, in time
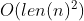
.
Proof
(q.e.d.)
Exercise 3.29. This exercise develops an algorithm to compute
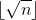
for a given positive integer
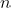
. Consider the following algorithm:
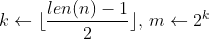
(a) Show that this algorithm correctly computes
.
(b) In a straightforward implementation of this algorithm, each loop iteration takes time
, yielding a total running time of
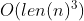
. Give a more careful implementation, so that each loop iteration takes time
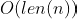
, yielding a total running time is
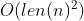
.
Proof
(q.e.d.)
Exercise 3.30. Modify the algorithm in the previous exercise so that given positive integers
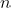
and

, with
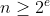
, it computes
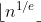
in time
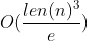
.
Proof
(q.e.d.)
Exercise 3.31. An integer
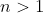
is called a perfect power if
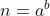
for some integers
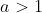
and
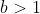
. Using the algorithm from the previous exercis, design an efficient algorithm that determines if a given
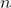
is perfect power, and if it is, also computes

and
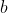
such that
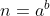
, where
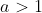
,
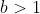
, and

is as small as possible. Your algorithm should run in time
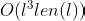
where
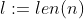
.
Proof
(q.e.d.)
Exercise 3.32. Show how to convert (in both directions) in time
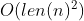
between the base-10 representation and our implementation's internal representation of an integer
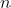
.
Proof
(q.e.d.)
